2012年國家公務員行測數學運算-3000頁碼里含有多少個2? 析:1-99里有20個2,100-199有20個2。0-999中,除了200-299有100+20個2以外,每100都有20個2,則0-999共有2:120+9*20=300 同理:3000-3999也有300個2 考慮2000-2999,因為0-999含有300個2,這1000個數里,每個數其實都多加了一個2,則應該含有1000+300個2。則共有2:1300+300+300。一般地:001-099有20個N(N表示1-9的任何數)100-199有20個N(N不能等于1) 200-299有20個N(N不能等于2)……0000-0999有300個N,1000-1999有300個N(N不能等于1)2000-2999有300個N(N不能等于2)……00000-09999有4000個N 10000-19999有4000個N(N不能等于1)100000-199999有50000個N(N不能等于1)900000-999999有50000個N(N不能等于9) 而: 100-199有120個1 1000-1999有1300個1 2000-2999有1300個2 10000-19999有14000個1 100000-199999有150000個1。
則此題中:思路1:0-999含2為300個,1000-1999含2為300個;2000-2999含2為1300個。則共有1900個2。思路2:0-3000中,百位以下(含百位)含2為,3*300=900,千位含2為1000個。則共有1900個2。例:一本1000頁的書有多少個1?析:1000頁書中,0-999頁有300個1,1000又有1個1,則共有301個1。例:一本10000頁的書有多少個1?析:0-9999有4000個1,加上10000的一個1,則為4001個1。例:3000頁的書有多少個3? 析:0-999有300個3,1000-1999有300個3,2000-2999有300個3,3000有1個3,則3*300+1=901頁
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
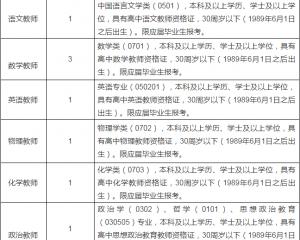 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12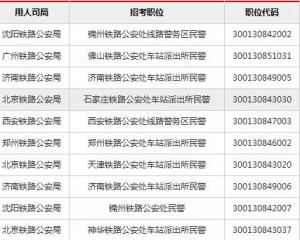 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31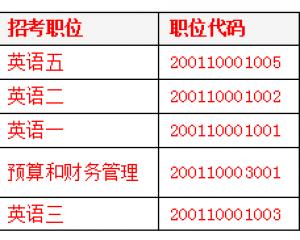 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31