2012年國家公務員行測數學運算-剩余定理原理用個例子解釋,一個數除以3余2,那么,這個數加3再除以3,余數還是2. 一個數除以5余3,除以4余3,那么這個數加上5和4的公倍數所得到的數,除3還是能得到這個結論。 例:一個三位數除以9余7,除以5余2,除以4余3,這樣的三位數共有() 析:7是最小的滿足條件的數。9,5,4的最小公倍數為180,則187是第二個這樣的數,367,547,727,907共5個三位數。 例:有一個年級的同學,每9人一排多5人,每7人一排多1人,每5人一排多2人,問這個年級至少有多少人? 析:題目轉化為,一個數除以9余5,除以7余1,除以5除2。第一步,從最大的數開刀,先找出除以9余5的最小數,14。 第二步,找出滿足每9人一排多5人,每7人一排多1人的最小的數。14除以7不余1;再試14+9這個數,23除以7照樣不余1;數取14+9*4時,50除以7余1,即滿足每9人一排多5人,每7人一排多1人的最小的數是,50; 第三步,找符合三個條件的。50除以5不余2,再來50+63(9,7的最小公倍數)=123,除5仍不余2;再來,50+126,不余2;……當50+63*4時,余2,滿足3個條件,即至少有302個人。
例:自然數P滿足下列條件:P除以10的余數為9,P除以9的余數為8,P除以8的余數為7.如果100<P<1000,則這樣的P有幾個?析:此題可用剩余定理。但有更簡單的,P+1是10的倍數P+1是9的倍數P+1是8的倍數1-1000內,10,9,8的公倍數為,360,720,則P為359,719。3.84*86=?出現如AB*AC=?,其中B+C=10,計算結果為:百位數為A(A+1),十位/個位數為:B*C。注:如果B*C小于10,用0補足。如:29*21,百位數為2*3=6,個倍數為1*9=9,則結果為609. 4.根號3,3次根號下5,哪個小?這類題,關鍵是用一個大次的根號包住兩個數。一個是2次根號,一個是3次根號,則應該用6次根號包住它們。根號3,可以化成6次根號下27;3次根號下5,可化為6次根號下25,則根號3大于3次根號下5.
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
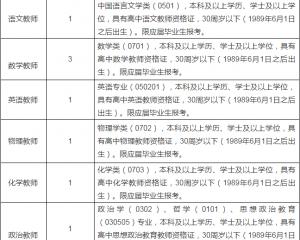 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12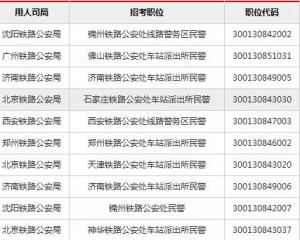 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31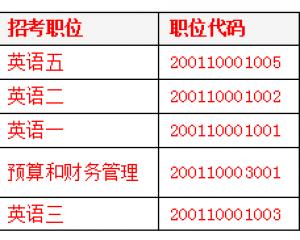 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31