數字特性法,顧名思義,就是利用數字的特性來做題。主要包括奇偶特性、整除特性、以及比例倍數特性。數字特性法是最能體現行測特點的方法,效率極高。本文重點介紹其中的整除特性。
以2013年國考第65題為例。某種漢堡包每個成本4.5元,售價10.5元,當天賣不完的漢堡包即不再出售。在過去十天里,餐廳每天都會準備200個漢堡包,其中有六天正好賣完,四天各剩余25個,問這十天該餐廳賣漢堡包共賺了多少元( )
A.10850 B.10950 C.11050 D.11350
此題屬于基礎經濟問題,可以列方程求解。但若運送數字特性思想,解題將更快捷。利潤=收入-成本=單個售價×賣出數量-單個成本×制作數量,單個售價為10.5元,含有3因子;單成本為4.5元,也含有3因子。因此兩者之差必然含有3因子。根據被3整除的特性——各位數字之和能被3整除,可迅速排出A、C、D,鎖定答案為B。
在解題過程中,當我們確定答案一定為某一個數的倍數時,可以嘗試采用整除特性。如下題:
一個班級租車出去游玩,租車費用平均每人30元,如果增加7個人,平均每人25元,求這個班級一共花了( )元。
A.1050 B.1100
C.950 D.1000
總花費必定為平均費用即30的倍數,排除B、C、D,快速鎖定答案為A。
實際上,在上題的解題過程中,我們一般會看選項是否為3的倍數(總花費為30的倍數,則其必定為3以及10的倍數)。因為在公務員考試中,考察較多的一般為3、9、11等的整除特性,其中3、9最常見。有時還會考察一個數除以3、9的余數規律。
以2011年廣西區考第43題為例。某單位招錄了10名新員工,按其應聘成績排名1到10,并用10個連續的四位自然數依次作為他們的工號。湊巧的是每個人的工號都能被他們的成績排名整除,問排名第三的員工工號所有數字之和是多少?
A. 9 B. 12
C. 15 D. 18
很明顯,第三名的員工工號必定為3的倍數,但選項A、B、C、D均為3的倍數,此路不通。因此若想求得數字之和,必定需要轉換思路,尋求與各位數字之和有關的另外一個規律——即9的倍數的聯系。第九名工號必定為9的倍數,即第三名的工號加上6為9的倍數,所以第三名的工號除以9余數為3,即第三名的工號的各位數字之和除以9余3。排除A、C、D,鎖定答案為B。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
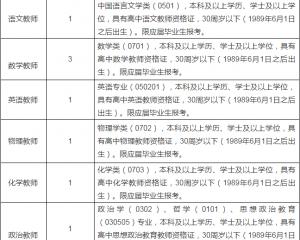 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12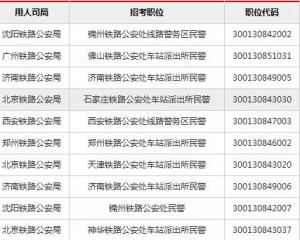 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31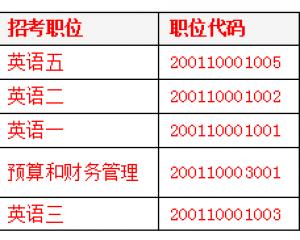 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31