相關資訊
-
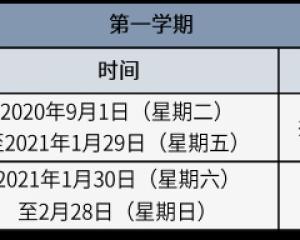 北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15 -

-
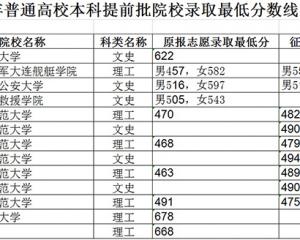 黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19
黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19 -
 交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10
交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10 -
 2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06
2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06