教育部考試中心已正式發布了2017年全國碩士研究生入學考試大綱,這雖然比原定的計劃整整提前了兩周,但在數學方面卻毫無驚喜,依舊和去年完全一致,所以同學們可以安心按原計劃復習備考。
從數學的復習情況來看,目前大家高等數學的復習已經較為充分,但很多同學在線性代數上卻找不到好的入手點,那么如何更高效的復習線代,在有限的時間內突破這門學科的瓶頸,并最終在考試中獲得高分呢?各位考生通過以下三個方面的閱讀學習一定會得到滿意答案的。
一、線性代數這門學科自身特點
與高數相比,線代這門課相對計算技巧較少,貫穿始終的計算方法幾乎只有初等變換這一種,但知識點卻比另兩門學科都要抽象的多。比如看到矩陣"秩"的概念時,同學們都會齊聲問道"這是什么鬼";接著又出現了線性相關、無關,極大線性無關組,同學們更是驚呼"線代有毒"。
其實這些概念如果大家能對應你相對熟悉的線性方程組就好理解多了。首先,大家可以體會下向量組的線性相關、無關其實是和齊次線性方程組有無非零解一一對應的。其次,矩陣的"秩"想說明的是方程組中本"質"方程或有效方程的個數,大家利用初等行變換化出的那些全零行,實際就是去掉那些"無效"方程組的過程;于是r(A)個有效方程只能限定r(A)個未知數,那么原有的n個未知數中就有n- r(A)個無法限定,所以稱為自由未知量,進一步就可以得到方程組解中的一組極大無關組,也就是我們說的基礎解系(利用最少的解向量去表示所有的解)。
類似地,大家還可以思考線性表示和非齊次線性方程組解之間的關系,這樣線代這些抽象的概念就會變得so easy,不懂哪里對比哪里!
二、線性代數知識結
基本概念--三大工具:行列式、矩陣、向量組;
基本計算--求解線性方程組;
簡單應用--利用方程組的解反過來研究矩陣的特征值、特征向量及對角化;還可以研究簡單的非線性組合關系即二次型的基本概念和性質。
大家學習過程中可以以矩陣為主線,具體展開復習。如行列式可以看成方陣的一種運算;解方程組的過程其實也主要利用的是矩陣的初等行變換;二次型的研究也主要是對其對應的二次型矩陣的變換等等。
還可以利用矩陣可逆的充要條件去串聯整個線性代數的前后章節,它們分別是:行列式不等于0;方陣是滿秩的;矩陣的行或列向量組組性無關;對應齊次線性方程組只有零解;矩陣沒有0特征值;正負慣性指數之和為n等;這樣大家就可以更簡潔明了的做到前后知識的融會貫通了。
三、線性代數重點題型解析
所有知識的復習都為了考試中取得好的成績,那么對重點題型的研究,則也顯得尤為關鍵。數學考試三個卷種,對線性代數的要求基本一致,大小題加一起也都是五道,而且可考的題型相對固定,尤其是兩道11分的計算大題,基本就是后三章的內容出兩道,而且解方程組的內容一定會涉及到的,所以大家對利用矩陣初等變換求解方程組一定要多練習,得做到準確快速。
但考查形式還是經歷了不少變化,首先從考研最初幾年直接求解方程組,到考討論含參數的方程組解,再到十年前關于兩個方程組公共解和同解的討論(如在05年和07年的大題中連續出現);然而近幾年命題人則更喜歡給方程組穿上外套,先是轉換成了向量組線性表示一個向量或向量組之間的相互線性表示(如11年的真題),然后又是通過矩陣方程對解方程組進行考察(如13,14年的20題,數一16年20題);但大家只要摸清了這些套路,其實萬變不離其中。
第二道大題則常考查矩陣對角化或二次型標準化的過程,并且近年也常結合矩陣間的三種(等價、相似、合同)關系共同命題,如15,16年21題就是對矩陣相似關系的考查,而矩陣的合同關系之前卻較少在大題中命題,所以同學們今年也可以多關注下矩陣間合同的內容。
我想同學們如果能從以上三個方面入手,結合大家在強化階段的講義和近年真題解析,進行更有針對性的復習備考,在最后的100多天復習時間里,在線性代數這門學科獲得質的提升,并取得高分甚至滿分還是希望很大的。
最后祝各位考生在強化和沖刺階段復習中漸入佳境,金榜題名!
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
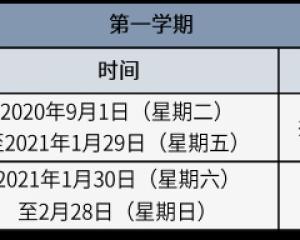 北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
北京中小學8月29日起分批錯峰開學 2021年1月30日放寒假-查字典資訊網2020-09-15
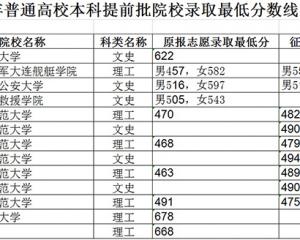 黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19
黑龍江:2020年普通高校本科提前批院校錄取最低分數線-查字典資訊網2020-08-19 交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10
交叉學科將成第14個門類,這些高校早已搶占先機!2020-08-10 2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06
2021考研招生簡章已公布?漢族考生也可享受“少干計劃”的降分優惠?-查字典資訊網2020-08-06