縱觀近年來的考題,經濟問題在考試中出現的頻次頗高,而題型也從過去簡單的利潤折扣問題變得越加多樣化,如分段計費,又如我們接下來要談到的花費統籌問題。花費統籌問題是一種更接地氣兒的經濟問題,即民眾再熟悉不過的商場優惠活動問題。
例1:某商場促銷,晚上八點以后全場商品在原來折扣基礎上再打9.5折,付款時滿400元再減100元,已知某鞋柜全場8.5折,某人晚上九點多去該鞋柜買了一雙鞋,花了384.5元,問這雙鞋的原價為多少錢?
A.550 B.600
C.650 D.700
解答這道題目需要注意兩點,一是所支付的384.5元是由何種優惠得來,即支付時是否滿400;二是題目所問為原價,即支付價格是在8.5折基礎上再打9.5折而來。首先考慮支付時不滿400元,那么原價為384.5÷0.85÷0.95≈476元(定價肯定是個整數);再考慮付款滿時滿400元,那么原價為(384.5+100)÷0.85÷0.95=600元,所以選B。
例2:某商場在進行“滿百省”活動,滿100省10,滿200省30,滿300省50。大于400的消費只能折算為等同于幾個100、200、300的加和。已知一位顧客買某款襯衫1件支付了175元,那么買3件這樣的襯衫最少需要()。
A. 445元 B. 475元
C. 505元 D. 515元
解答此題的誤區在于“一位顧客買某款襯衫1件支付了175元”,并非告訴我們襯衫的價格就是175元,而需要我們還原原價。因此較例1相比,此題不但需要找出原價,還需要在此基礎上找出最省錢的方案。與例1一樣,先考慮支付175元時是否滿200元,若未滿則原單價為185、總價為555元;若滿200,則原單價為205,原總價為615元。在選取優惠方案時,顯然是金額越大省得越多,所以555元分別按300、200的方案支付,則最后需付250+170+55=475元;615元按兩個300的方案支付,最后需付250+250+15=515元。題目要求最少,則選取475元即可。
例3:某商場開展購物優惠活動:一次購買300元及以下的商品九折優惠;一次購買超過300元的商品,其中300元九折優惠,超過300元的部分八折優惠。小王購物第一次付款144元,第二次又付款310元。如果他一次購買并付款,可以節省多少元?
A.16 B.22.4
C.30.6 D.48
小王第一次付款金額144元由原價打9折而來,因而原價為144÷0.9=160元。第二次付款超過300元,需分段考慮。首先原價300以下的部分實際支付300×0.9=270元,可知多出的310-270=40元由原金額打8折而來,這部分金額為40÷0.8=50元,所以商品原價為300+50=350元。若一次性購買,總價為160+350=510元,需支付300×0.9+210×0.8=438,比144+310=454節省了16元。當然也可以這么思考,節省的錢來自于原價160的商品折扣從原來的9折變為8折,節省了160×0.1=16元。
從上面幾個例子可以看出,其實花費統籌問題并不難,只需要把題目所給的優惠條件理清楚,在此基礎上注意兩點即可:一是弄清哪種方案最優惠,二是避免直接將“支付價格”默認為原價。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
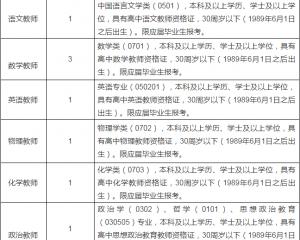 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12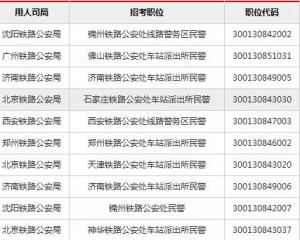 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31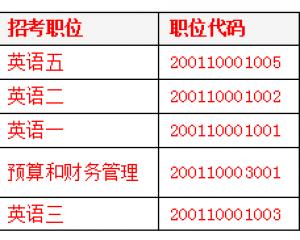 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31