【1】一列快車和一列慢車相對而行,其中快車的車長200米,慢車的車長250米,坐在慢車上的旅客看到快車駛過其所在窗口的時間是6秒鐘,坐在快車上的旅客看到慢車駛過其所在窗口的時間是多少秒鐘?
A.6秒鐘 B.6.5秒鐘 C.7秒鐘 D.7.5秒鐘
【2】有8種顏色的小球,數量分別為2、3、4、5、6、7、8、9,將它們放進一個袋子里面,問拿到同顏色的球最多需要幾次??
A.6 B.7 C.8 D.9
【3】已知2008被一些自然數去除,得到的余數都是10,那么,這些自然數共有( )
A.10 B.11 C.12 D.9
【4】真分數a/7化為小數后,如果從小數點后第一位數字開始連續若干數字之和是1992,那么A的值是( )
A.6 B.5 C.7 D.8
【5】從1到500的所有自然數中,不含有數字4的自然數有多少個?( )。
A.323 B.324 C.325 D.326
解析
【1】分析:選D,追擊問題的一種。坐在慢車看快車=>可以假定慢車不動,此時,快車相對速度為V(快)+V(慢),走的路程為快車車長200;同理坐在快車看慢車,走的距離為250,由于兩者的相對速度相同=>250/x=200/6=>x=7.5(令x為需用時間)
【2】分析:選D,“抽屜原理”問題。先從最不利的情況入手,最不利的情況也就使次數最多的情況。即8種小球,每次取一個,且種類不相同 (這就是最不利的情況)。然后任取一個,必有重復的,所以是最多取9個。
【3】 分析:答:選B, 余10=>說明2008-10=1998都能被這些數整除。同時,1998 = 2×3×3×3×37,所以 ,取1個數有 37 ,2,3。 --- 3個。,只取2個數乘積有 3×37,2×37, 3×3,2 ×3。--- 4個。,只取3個數乘積有 3×3×37,2×3×37,3×3×3,2×3×3 。--- 4個。只取4個數乘積有 3×3×3×37,2×3×3×37,2×3×3×3。 --- 3個。只取5個數乘積有 2×3×3×3×37 --- 1個。總共3+4+4+3+1=15,但根據余數小于除數的原理,余數為10,因此所有能除2008且余10的數,都應大于10=>2,3, 3×3, 2×3被排除。綜上,總共有3+4+4+3+1-4=11個
【4】分析:答:選A, 由于除7不能整除的的數結果會是‘142857’的循環(這個可以自己測算一下),1+4+2+8+5+7=27,1992/27 余數為21,重循環里邊可知8+5+7+1=21,所以8571會多算一遍(多重復的一遍,一定在靠近小數點的位置上),則小數點后第一位為8,因此a為6。
【5】分析:答:選B, 把一位數看成是前面有兩個0的三位數,如:把1看成是001.把兩位數看成是前面有一個0的三位數。如:把11看成011.那么所有的從1到500的自然數都可以看成是“三位數”,除去500外,考慮不含有4的這樣的“三位數”.百位上,有0、1、2、3這四種選法;十位上,有0、1、2、3、5、6、7、8、9這九種選法;個位上,也有九種選法.所以,除500外,有C(1,4)×C(1,9)×C(1,9)=4×9×9=324個不含4的“三位數”.注意到,這里面有一個數是000,應該去掉.而500還沒有算進去,應該加進去.所以,從1到500中,不含4的自然數有324-1+1=324個
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
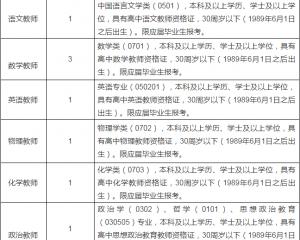 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12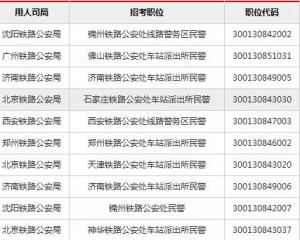 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31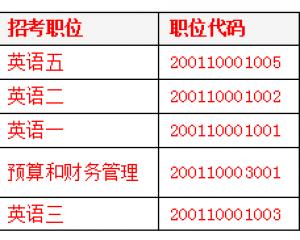 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31