NewsContent"
山東公務員考試行測數量關系-【391】從自然數列1,2,3,4......中依次劃去2的倍數和3的倍數,但保留5的倍數,剩下的數列如下:1,5,7,10,11,13,15,17,19,20,23,25,29......在剩下的數列中,第2005個數是幾?
公務員考試網分析:第2005個數滿足這樣的條件,設它為n,則n-[n/2]-[n/3]+[n/6]+[n/10]+[n/15]-[n/30]=2005, (其中[n/k]表示不超過n/k的最大整數,對于正數,相當于取它整數部分。) 首先估計一下范圍: n-n/2-n/3+n/6+n/10+n/15-n/30=2005, 解得n大概為:4296,將4296代入:4296-[4296/2]-[4296/3]+[4296/6]+[4296/10]+[4296/15]-[4296/30]=4296-2148-1432+716+429+286-143=2004,比2005小1,取4297,代入,發現[ ]內的值與4296時都一樣,所以結果正好是2005,所以第2005個數是4297.
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
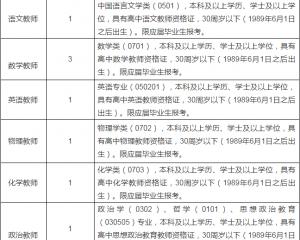 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12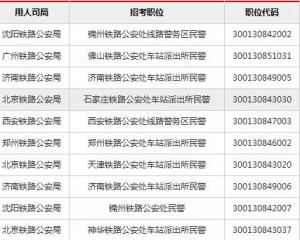 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31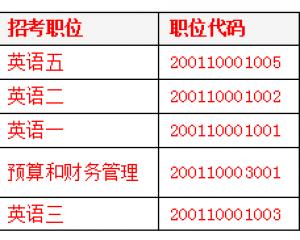 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31