概念介紹
其實,日常邏輯和形式邏輯不同,很多我們日常邏輯中遇到的覺得沒問題的邏輯關系,用形式邏輯一推理,就說不通了。舉個最常見的例子:一群邏輯學家去亞里士多德學院開邏輯學大會,會場門口豎了一塊牌子“不懂邏輯者不得入內”,這時候,邏輯學家們開始議論紛紛:“我們都是懂邏輯的人,到底是進還是不進?”這個問題如果用我們日常邏輯的思路,可能就會想,不懂邏輯者不得入內,那我們是懂邏輯的,自然就可以入內的了。可事實上,要是按照我們形式邏輯來推理,不懂邏輯者不得入內等價于入內者都懂邏輯,但是卻不能等價于懂邏輯者可以入內。細細體味,二者還是有很大差別的。
考試當中一般常見的邏輯關系,分為等價關系和集合關系。等價關系里又分為逆否等價和摩根等價,本文中,將就逆否等價關系跟大家做一個分享:逆否等價是等價命題中最基礎也是最常見的等價形式,他是在表述這樣一種等價關系:命題P→Q等價于-Q→ -P
等價命題非常好理解,例如如果天下雨,那么地就濕表達的邏輯關系是“天下雨→地就濕”,該命題等價于“如果地沒濕,那么天沒下雨”。這是非常好理解的。但是需要注意,如果天沒下雨,地會不會濕呢?這個是不一定的。再者,如果地濕了,天有沒有下雨這個也是不一定的,這就提示我們注意,在等價命題中,-P無法推出Q或-Q,同樣-Q也無法推出P或-P。這也就是前述那個例子中為什么懂邏輯也不一定能入內的邏輯學道理。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
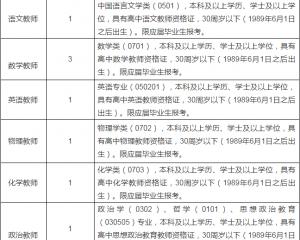 江西師范大學附屬中學2020年招聘教師2020-06-24
江西師范大學附屬中學2020年招聘教師2020-06-24 上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:952020-06-12 上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12
上海公務員考試《行測》通關模擬試題及答案解析【2019】:632020-06-12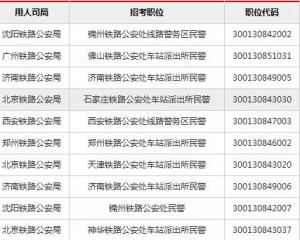 2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31
2019國考報名人數統計:鐵路公安系統過審超6萬 競爭力度較高【截至29日16時】2018-10-31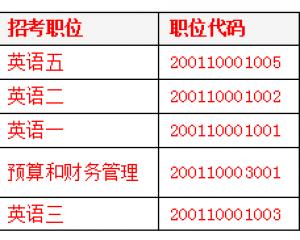 2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31
2019國考報名外交部過審3萬余人 平均7人爭一職2018-10-31