中考數學考試知識點分析:反比列函數
小編導語:每一門功課都有它自身的規律,有它自身的特點,數學當然也不例外。下面是有關中考數學考試知識點分析:反比列函數的內容,供你學習參考!
反比例函數的定義
定義:形如函數y=k/x(k為常數且k≠0)叫做反比例函數,其中k叫做比例系數,x是自變量,y是自變量x的函數,x的取值范圍是不等于0的一切實數。
反比例函數的性質
函數y=k/x 稱為反比例函數,其中k≠0,其中X是自變量,
1.當k>0時,圖象分別位于第一、三象限,同一個象限內,y隨x的增大而減小;當k<0時,圖象分別位于二、四象限,同一個象限內,y隨x的增大而增大。
2.k>0時,函數在x<0 x="">0上同為減函數;k<0時,函數在x<0 x="">0上同為增函數。
3.x的取值范圍是: x≠0;
y的取值范圍是:y≠0。
4..因為在y=k/x(k≠0)中,x不能為0,y也不能為0,所以反比例函數的圖象不可能與x軸相交,也不可能與y軸相交。 但隨著x無限增大或是無限減少,函數值無限趨近于0,故圖像無限接近于x軸
5. 反比例函數的圖象既是軸對稱圖形,又是中心對稱圖形,它有兩條對稱軸 y=x y=-x(即第一三,二四象限角平分線),對稱中心是坐標原點。
反比例函數的一般形式
一般地,如果兩個變量x、y之間的關系可以表示成
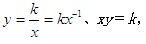
(k為常數,k≠0)的形式,那么稱y是x的反比例函數。
其中,x是自變量,y是函數。由于x在分母上,故取x≠0的一切實數,看函數y的取值范圍,因為k≠0,且x≠0,所以函數值y也不可能為0。
補充說明:1.反比例函數的解析式又可以寫成: (k是常數,k≠0).
2.要求出反比例函數的解析式,利用待定系數法求出k即可.
反比例函數解析式的特征
⑴等號左邊是函數,等號右邊是一個分式。分子是不為零的常數(也叫做比例系數),分母中含有自變量,且指數為1。
⑵比例系數
⑶自變量的取值為一切非零實數。
⑷函數的取值是一切非零實數。

反比列函數與一次函數圖像的交點

用反比例函數求面積應用

反比例關系與反比例函數的區別和聯系

更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!