對于數學運算中的基本思想之一“數的整除思想”既是重點也是難點還是考點。對于“數的整除思想”,首先我們要知道其概念,這里重點強調一下,對于數的整除必須要求“除數、被除數、商必須都是整數(余數為0)”。除此之外還要重點和一個相似的概念區分開來。"除盡"主要是指兩個數相除得到的余數為0,商不是一個無限循環的數。在做題之前一定要將概念理解了,在理解的基礎上進一步掌握特性和技巧。做到:懂概念,做地基。握技巧,速解題。攻計算,百分百。
下面事業單位考試研究院溫琪老師,將結合例題為考生講解如何運用數學運算中的整除技巧。
題型二:
某校三年級同學,每11人一排多5人,每7人一排多1人,每5人一排多2人,問這個年級至少有多少人?
A.187 B.202 C.237 D.302
中公解析:D。解析:根據題意,每11個人一排則多5人,可得正確選項必滿足減去5能夠被11整除,根據11的整除特性可知,只有D項滿足條件,選擇D。
名師點撥:此題的關鍵在于兩點。一是,將余數轉化為整除。二是,利用11的整除特性。
題型三:
50名同學面向老師站成一行。老師先讓大家從左至右按1,2,3,…依次報數;再讓報數是4的倍數的同學向后轉,接著又讓報數是6的倍數的同學向后轉。現在面向老師的同學還有( )。
A.30人 B.34人 C.36人 D.38人
中公解析:D。解析:只有轉動一次的同學才背對著老師,轉動兩次或者沒有轉動的同學是面向老師的。50以內的數中4最大的倍數是48,故4的倍數的個數有48÷4=12;50以內的數中6的最大的倍數是48,故6的倍數的個數有48÷6=8;既是4的倍數,又是6的倍數的個數有12、24、36、48共4個,故發生轉動的同學有12+8-4=16人,其中4人轉了兩次,故只有16-4=12人轉動了一次,面向老師的同學有50-12=38人。
名師點撥:綜合來看這道題既可以看做是整除的應用又可以看做容斥問題,包含的知識點比較多,但是,解題的關鍵在于先求出在某個范圍內被除的數有幾個再進一步分析。
整除的利用不在于多么的復雜,而在于對技巧應用的把握,在做題過程中可以慢慢的積累繼而得到提升。
更多精彩資訊請關注查字典資訊網,我們將持續為您更新最新資訊!
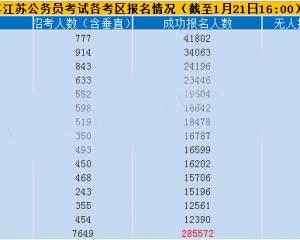 2017年江蘇公務員考試最終285572人成功報名2017-01-22
2017年江蘇公務員考試最終285572人成功報名2017-01-22 2016下半年四川公務員考試面試時間暫定3月2017-01-20
2016下半年四川公務員考試面試時間暫定3月2017-01-20 2017年江蘇公務員考試資格初審將于20日結束2017-01-20
2017年江蘇公務員考試資格初審將于20日結束2017-01-20 2017年北京延慶區大學生村官|選調生考試調劑公告2017-01-19
2017年北京延慶區大學生村官|選調生考試調劑公告2017-01-19 2017北京民防局公務員考試調劑公告2017-01-18
2017北京民防局公務員考試調劑公告2017-01-18